[번역] 선형 회귀 모델 Bayesians vs Frequentists

이번 포스트는 다음 글 From both sides now: the math of linear regression을 읽고 frequentist와 bayesian 관점에서의 선형 회귀모델을 잘 정리한 것 같아 번역해 보았습니다. 대학원 때 MLE를 구하는 방법으로, 미분의 해로 구하는 방법, Gradient Decent 방법으로 푸는 방법, 선형대수의 Project Matrix를 통해 구하는 방법 등 참 여러가지 방법으로 선형 회귀 모델에 대해서 이해하고 배웠던 점이 무척 재밌었습니다. 이번에는 모수를 추정하는 다른 두 관점에서 선형 회귀을 설명한 글을 읽게 되어 복습하는 마음에서 번역해 보았습니다.

선형회귀 모델은 기계학습에서 가장 기본적이고 널리 쓰이는 기술입니다. 자주 쓰이고 간단한 기술이지만 통계학의 아주 중요한 개념들을 배울 수 있습니다.

만약 여러분이 \(\hat{Y} = \theta_0 + \theta_1X\) 와 같은 선형 회귀 식에 대한 기본적인 이해는 있지만 Ridge 선형 회귀가 사실은 zero-mean 정규분포의 사전분포를 가진 MAP(Maximum A Posteriori) 추정치와 동일하다는 말을 잘 이해하지 못한다면, 이 글이 당신에게 딱 맞을 것입니다. (저 또한 마찬가지로 얼마전까지는 이 둘의 차이를 이해하지 못했었습니다.) 방금 얘기한 이 문장을 이해하기 위해 우리는 가장 기본적인 선형회귀부터 시작하여 확률론적 접근 관점(Probabilistic approach)에 대해서 얘기해 보고(maximum likelihood formulation) 마지막으로는 베이지안 선형회귀에 대해서도 얘기해 볼 예정입니다.

먼저 \(\theta\)를 앞으로 회귀 모델의 가중치라고 표기하겠습니다. 간혹 명확히 \(\theta_0\)와 \(\theta_1\)를 분리하여 기울기와 절편으로 나누어서 설명하기도 하고 전체를 합쳐서 \(\theta\)를 모델의 가중치 벡터라고도 표기하겠습니다. 또한 \(\theta^Tx_i\)를 \(x_i\)가 주어졌을 때의 모델의 예측값으로 표기하겠습니다. 이는 \(y\) 절편이 \(\theta\)안에 포함되어 있다는 가정입니다.

선에서 무엇을 알 수 있나요?

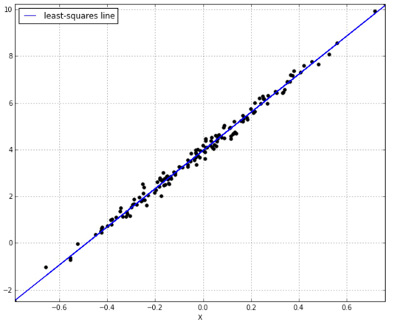
단변량 선형회귀인 경우, 우리는 최소 승자법(least squares fit)을 만족하는 선이 실측값과 예측값의 차이의 합을 최소화 한다는 것을 알고 있습니다. Residual Sum of Squares:

이때,

가 \(i\)번째 입력의 예측값인 것을 알 수 있습니다. 그리고 우리는 \(i\)번째 입력의 실제값을 다음과 같이 정의할 수 있습니다.

여기서 \(\epsilon_i\) 을 잔차 (residual), 혹은 오차라고 할 수 있습니다. 이것은 예측값 \(\hat{y_i}\) 과 실제값 \(y_i\) 와의 차이라고 말할 수 있습니다. 이 잔차는 앞으로 우리의 모델을 설계할 때 중요한 요소가 될 것입니다. 지금으로서는 잔차의 평균값이 (Expected value) 0이 되어야 한다고만 생각하시면 됩니다.

우리가 이 선에서 어떤 것을 더 알아 볼 수 있을까요? 바로 이 선이 예측치와 결과값간에 특별한 관계를 정의하는 것을 알 수 있습니다. 특히 선의 기울기가 예측값과 결과값과의 상관관계를 결정합니다. 이것은 학습 데이터를 통해 \(\theta_1\)를 계산할 수 있습니다. \(\theta_0\)의 경우에는 어떻게 할까요? 우리는 이 선이 \(\bar{x}, \bar{y}\)의 점을 지난다는 것을 압니다. 그렇기 때문에 우리가 선의 기울기만 알면 \(\theta_0 = \bar{y} - \theta_1\bar{x}\)와 같은 식을 통해 절편을 알 수 있습니다.

p개의 변수를 가지는 다변량 선형 회귀 모델인 경우, 우리는 다음과 같이 모델링 할 수 있습니다.

이러한 경우에는 단변량 선형 회귀 모델처럼 단순하게 모델의 계수를 찾기 쉽지 않습니다. 그 대신, 우리는 미적분학을 통해 다변량 모델의 목적 함수의 편미분를 구한 다음 그것을 0으로 놓고 계수의 해를 구하면 됩니다.

최적문제: 잔차 최소화에서 우도 최대화

만약 여러분이 베이지안 관점에서 선형회귀를 이해하길 원하신다면 이제 확률에 대해서 고민해 보길 바랍니다. 생각을 조금 바꿔 이제는 잔차의 차이를 줄이려고 생각하는 대신 관측 데이터의 우도를 최대화 시키는 방법에 대해서 고민해 봅시다. 뒤에 가서 보면 알겠지만 이것은 사실 같은 말입니다. 수학적으로 보자면, 이것은 동일한 해법을 서로 다른 관점에서 바라 보는 것뿐 입니다.

그럼 이제 우도를 계산해 봅시다. 어떤 모수를 가정하여 관측된 데이터의 우도를 파악하려면, 각 데이터 포인트 \(y_i\)의 확률을 전부 곱해야 합니다.

여기서 우리에게 최대우도값을 갖게 해줄 모수 (\(\theta\))를 찾는 것이 목표입니다. 그렇다면 각각의 확률을 어떻게 계산할 수 있을까요?

그대 정규분포를 알라

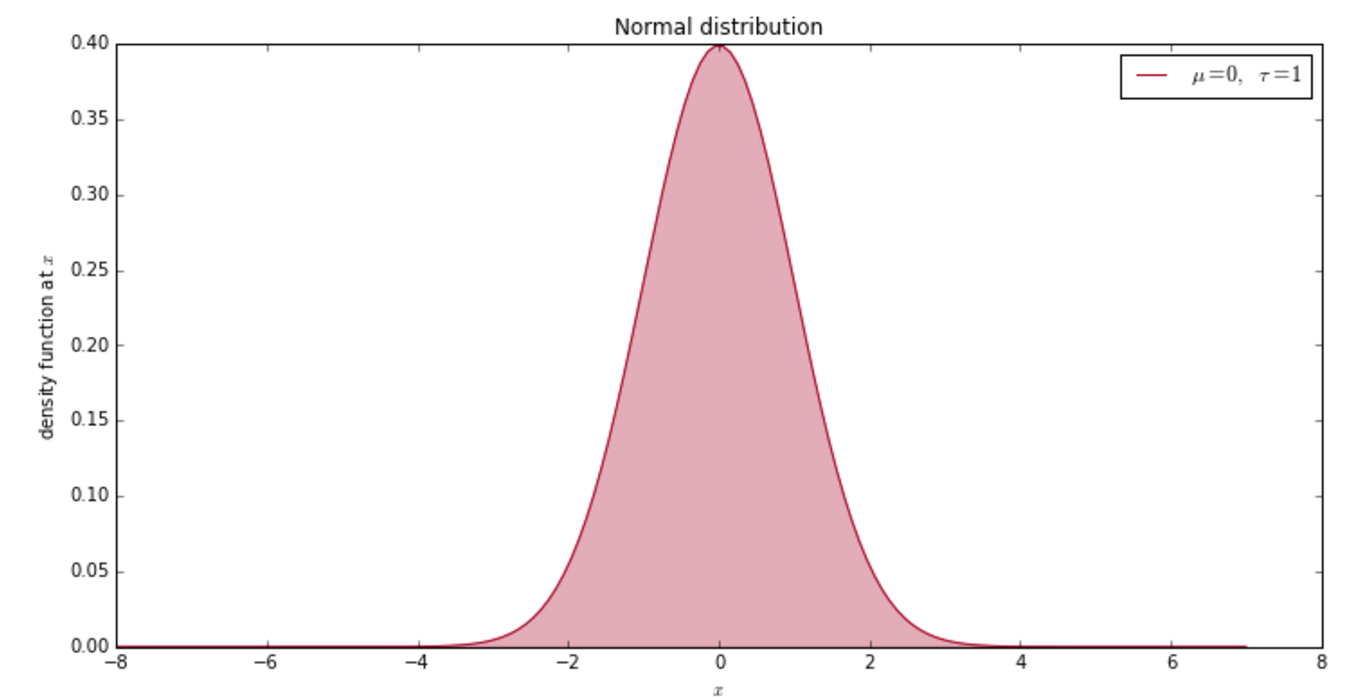
앞써 최소승자법에서의 잔차의 평균이 0이 된다는 것을 얘기했습니다. 조금 더 나아가서 잔차란 정규분포를 따르고 그 평균이 0인 노이즈라고 얘기해 봅시다.

아래의 수식이 정규분포, 즉 가우시안 분포를 나타내는 함수입니다:

그리 간단해 보이는 수식은 아니지만 꼭 알아야 하는 식입니다. 왜냐하면 여러 식에서 자주 나오기 때문입니다. 정규분포에서 유용한 사실 중 하나로 다음과 같이 쓸 수 있습니다.

\(X \sim \mathcal{N}(\mu, \sigma^2)\) and \(Y \sim \mathcal{N}(\mu, \sigma^2)\) then \(X = \mu + Y\)

다시 \(y\)값의 확률을 계산하는 것으로 돌아와서 \(y_i\) 는 \(\theta^Tx_i + \epsilon_i\) 라고 표현할 수 있고 노이즈 \(\epsilon_i\)가 정규분포를 따를때 (\(\epsilon_i \sim \mathcal{N}(0, \sigma^2)\))

라고 식을 바꿀 수 있습니다. 어떻게 수정했는지 알아 보시겠나요? 앞써 보여드린 정규분포의 변환을 거꾸로 적용하였습니다. 이로써 우리는 각 \(y_i\)를 확률적으로 계산할 수 있는 모델을 가지게 되었습니다. 이제 데이터를 가지고 모델의 평균과 분산을 구하기만 하면 됩니다. 아래의 코드는 \(x\)값이 주어졌을 때, 모수 (모델변수) \(\theta_0\), \(\theta_1\)과 편차를 가지고 \(y\)의 우도를 계산하는 수식을 파이썬으로 나타낸 함수입니다.

def log_likelihood(x, y, theta0, theta1, stdev):
    # Get the likelihood of y given the least squares model described
    # by theta0, theta1 and the standard deviation of the error term.
    for i, x_val in enumerate(x):
        mu = theta0 + (theta1*x_val)
        # This is just plugging our observed y value into the normal
        # density function.
        lk = stats.norm(mu, stdev).pdf(y[i])
        res = lk if i == 0 else lk * res
    return Decimal(res).ln()

사람들이 우도를 구할때 주로 단순한 우도 보다는 로그 우도를 구합니다. 왜냐하면 로그 우도가 통상 더 쉽게 구할 수 있거나 서로 비교하기에 더 편리하게 때문입니다. 로그 함수는 단조 증가 함수 이기 때문에 로그 우도를 최대화 시키는 지점이 원래의 우도에서도 동일한 합니다.

이제 우리의 목표는 \(\theta\)에 대해서 주어진 데이터의 우도를 최대화하는 것입니다. 아래는 정규분포의 곱으로 우도를 나타낸 식입니다.

약간의 수학적 트릭을 통해 위의 식을 아래와 같이 바꿀 수 있습니다. (\(e^xe^y = e^{x + y}\))

혹시 위의 식 중에서 어딘가 비슷해 보이는 부분이 보이시나요? 네 맞습니다. 바로 앞써 구한 RSS입니다! 보시다시피 빨간색으로 칠해진 부분을 최소화하는 것이 바로 전체 식을 최대화하는 것을 확인할 수 있습니다. 다른 말로 잔차의 제곱합을 최소화 시키는 것이 우도를 최대화 시키는 것과 동일하다는 것을 얘기합니다.

아래의 그래프에서 우도의 모양이 어떻게 나오는지 확인해 보시기 바랍니다.

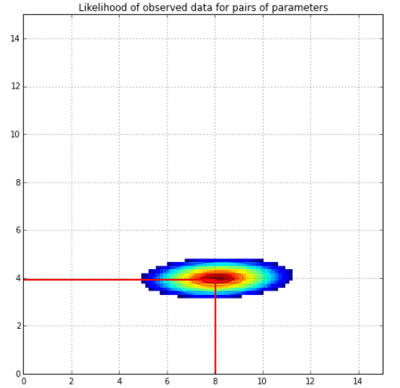
이것은 선형회귀 모수를 그린 그래프입니다. 각 \(X\)와 \(Y\)를 가지고 만들 수 있는 \((\theta_0,\theta_1)\)의 조합을 로그 우도 함수를 이용하여 그렸습니다. 실제 모델은 기울기 4에 절편 8인 1차식입니다. (\(y = 4 + 8x\))

베이지안 추론

지금까지 우도에 대해서 알아보았고 이제 베이지안 방법론에 대해서 얘기해 보겠습니다.

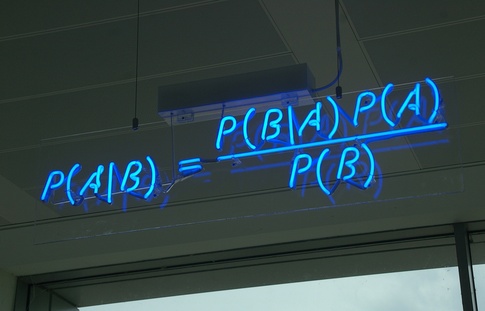
예전에 베이즈 룰에 대해 배운 것을 기억하시나요? 그것은 이벤트 B가 주어졌을 때의 이벤트 A의 확률을 나타냅니다.

여기에서 오른쪽식의 아래 분모 부분을 살펴보겠습니다. 분모에서 식을 간추려 보면 결국 \(p(B)\)로 단순화할 수 있습니다. 이를 이벤트 A가 “주변화” (marginalized out) 되었다고 말합니다. (이산 확률인 경우, 각 A, B에 대한 결합 확률을 적고 주변 (마지막) 컬럼에 전체 합을 구한 값을 넣게 때문에 주변화(marginalized) 되었다고 합니다.) 이러한 이유로 \(p(B)\)라는 확률을 주변 우도 (marginal likelihood) 라고 부릅니다. 또한 이 확률을 이벤트 A와 연관이 없기 때문에 때로는 아예 빼고 비율로만 계산하기도 합니다.

베이즈 룰이 베이지안 추론에서 사용되는 방법은 바로 주어진 데이터의 조건부 확률로 모델이 표현 된다는 것입니다.

여기서 \(H\)는 가설, \(D\)는 데이터를 나타냅니다. 간혹 데이터 대신 evidence라고 하기도 합니다. 베이즈 룰을 이러한 방식으로 해석함으로써, 드디어 사전분포와 사후분포에 대해서 얘기할 수 있게 되었습니다. 베이지안 세계에서 확률이란 용어는 가설에 대한 믿음의 측도로 사용됩니다. 먼저 사전 믿음을 가지고 가설을 바라보고 이후에 데이터를 관측하면, (이벤트 확보) 관측된 데이터를 가지고 새롭게 사후 믿음을 업데이트합니다.

혹은

한가지 베이지안 방법론에서 중요하게 짚고 가고 싶은 점은, 베이지안 방법론에서는 항상 불확실성에 대해서 얘기한다는 것입니다. 베이지안에서는 점추정이 아니라 확률분포를 따집니다. 그렇기 때문에 선형회귀 모델의 파라미터에 대한 가설을 점추정 (“절편의 값이 4일 것이야”)하지 않고 “평균이 4이고 어떤 분산으로 되어 있는 정규분포로 파라미터가 분포되어 있어” 라고 말합니다. 그리고 이것은 데이터가 많아질수록 지속적으로 업데이트가 됩니다. 이는 베이지안에서 사전분포가 확률분포(distribution) 로 표현되기 때문에 사후분포도 확률분포로 표현되기 때문입니다.

저는 이것을 다음과 같이 표현하길 좋아합니다. 데이터가 마치 확률분포를 잡아 당기는 자석과 같다고 말이죠.

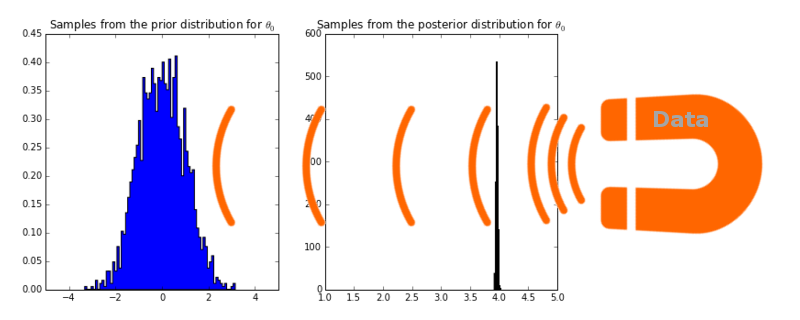
왼쪽 그림은 절편 부분의 모수에 대한 사전분포에서 샘플링한 그래프를 나타냅니다. \(\theta_0\): 평균 0, 분산 1인 표준 정규분포입니다. 이것을 PyMC (MCMC를 시뮬레이션할 수 있는 파이썬 라이브러리입니다.)를 이용하여 사후분포를 샘플링한 것이 오른쪽 그림입니다. 새롭게 업데이터된 분포에서 평균은 3.95로 실제 파라미터 값 4와 가깝습니다. 이것이 \(\theta_0\)에 대한 Maximum A Posteriori (MAP) 추정값입니다.

MAP 추정값이 ridge 선형회귀모델과 어떤 관계가 있는지 더 알아보기 전에 베이지안 관점에서 회귀모델에 대해 조금 더 설명하고자 합니다. 만약에 사전분포를 정규분포가 아닌 uniform 확률분포 (-2 ~ 2)로 설정하면 어떻게 될까요?

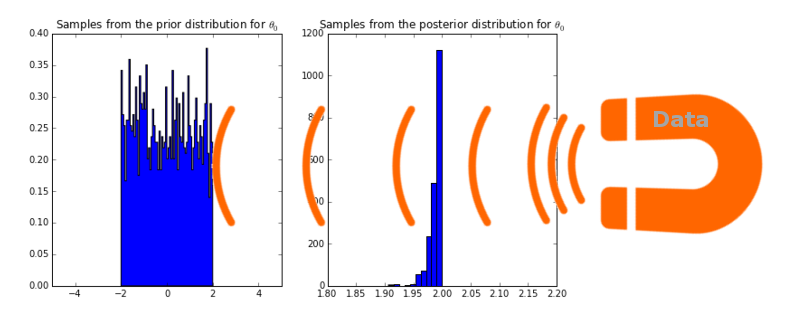
위의 그래프를 보시면 데이터 자석의 힘을 얼마나 강하게 만들어도 (다시 말해 얼마나 많은 데이터를 훈련시켜도) 사후분포는 절대로 2보다 더 큰 값에 확률을 부여하지 않습니다. (2 이상의 확률이 전부 0) 이것은 다시 말에 사전확률을 선택하는 것이 굉장히 중요하다는 것을 의미합니다.

일단 전체 모수에 대해 사후확률을 갖게 되면, MAP 추정값을 모수에 집어 넣어서 새로운 데이터에 대해 예측값을 뽑아낼 수 있습니다:

여기서 \(x^*\)는 새로운 데이터이고 \(y^*\)는 예측하려고 하는 값입니다. 이것이 바로 frequentist가 생각하는 방법입니다. 반면에 bayesian에서는 단순히 점추정 뿐만 아니라 분포를 활용할 수 있습니다. 그렇기 때문에 MAP 추정치에 대해 신뢰구간을 따로 얘기하지 않죠. 그 대신 예측값에 대한 확률분포를 가질 수 있게 됩니다. 베이지안에서는 모수에 대한 사후분포를 이용하여 새로운 데이터 \(x^*\)가 들어 왔을때 가질 수 있는 모든 결과값을 도출하고 확률분포 만큼의 가중치를 곱하여 최종 예측값을 얻어냅니다.

\(X\)와 \(Y\)는 학습 데이터로 주어지고, 예측하고자 하는 새로운 데이터 \(x^*\)도 주어집니다. 이렇게 3가지 데이터가 주어지면 최종적으로 얻고자 하는 \(y^*\)을 예측합니다. 그리고 이것을 \(\theta\)에 대해 사후분포를 주변화(marginalizing)하여 결과를 얻습니다. 이를 통해 \(x^*\)값에 따라 특정 분산을 가진 정규분포를 예측값으로 얻을 수 있습니다. (\(x^*\) 값이 학습 데이터에서 멀어질수록 분산이 커집니다.)

이렇게 함으로써 예측치에 대한 단순값 뿐만 아니라 불확실성의 정도까지도 알 수 있게 됩니다.

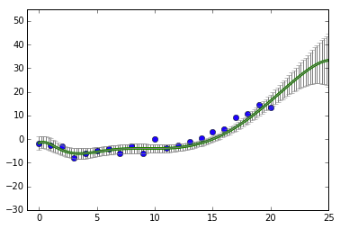
지금까지 학습한 데이터에서 벗어난 값일수록 그 불확실성이 더 커지겠죠.

저는 모르는 것을 알고 있다고 착각하여 잘못된 결정을 내리는 것보다는 모르는 것을 얼마나 모르는지 파악하는게 더 좋다고 생각합니다. 하지만 사람들은 어떤 질문에 대한 답을 얘기할 수 있는 것 자체를 더 선호하고 그 답이 얼마나 정확한 것인가에 대해서는 크게 걱정하지 않는 다는 사실에 놀라긴 하였습니다. 아마 그런 사람들은 자신이 어떤 얘기를 하는지 알지 못한 채 엄청난 자신감을 가지고 얘기하는 사람들일 것입니다. 개인적으로 저는 의심 많은 현자들과 얘기하는 것을 더 선호합니다. 이 점이 저를 베이지안으로 만든 것 같습니다.

(*역자주: frequentist와 bayesian에 대해 비교할 때 조금 강하게 본인의 의견을 적은 것으로 보입니다. 역자의 생각과 상관 없이 원글 그대로 번역하였습니다.)

MAP 추정치와 Ridge 선형회귀

이제 Ridge 선형회귀 모델과 MAP 추정치의 관계에 대해서 얘기할 때가 왔습니다. Ridge 선형회귀는 학습 데이터에 대한 과적합을 막기 위해 큰 값을 가진 모수(\(\theta\))에 패널티를 주는 모델입니다. 여기 Kevin Murphy의 머신러닝 책에 나와있는 코드 예시입니다. 이차 다항식으로 생성된 더미 데이터를 그려봤습니다. (\(y = ax + bx^2\)) 하지만 14차원 다항식의 모델로 데이터를 학습하였습니다. 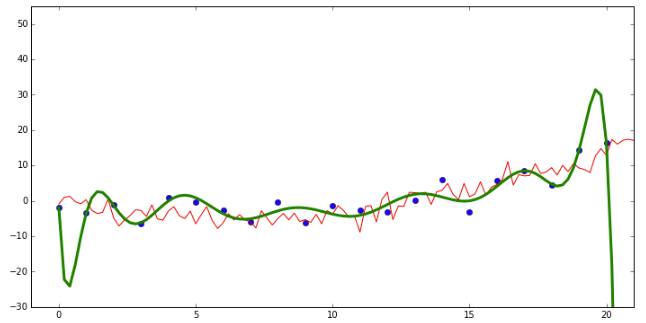초록색 선이 생성된 데이터로 학습한 모델을 가지고 예측을 하는 선입니다. 빨간색선이 실제 데이터의 값을 나타냅니다. 보시다시피 초록색선이 굉장히 굽어진 선으로 데이터를 잘 맞춥니다. 이것은 학습된 파라미터가 굉장히 큰 양수의 값이나 음수의 값을 갖기 때문입니다. 이런 경우 새로운 테스트 데이터에 대해서는 굉장히 못 맞추게 됩니다.(overfitting) 만약 모수에 극단적으로 큰 수를 가지는 것에 패널티를 주게 된다면 모델로 하여금 보지 못한 데이터 (unseen data)에 대해서도 잘 맞출수 있도록 강제할 수 있습니다. Ridge 회귀 모델에서는 파라미터의 제곱합을 비용 함수(coss function)에 추가함으로써 패널티를 줍니다.

이때 \(\lambda\)는 어떤 인자에 얼마 만큼의 패널티를 줄지를 결정하고 \(p\)는 파라미터 백터 \(\theta\)의 길이를 나타냅니다. Ridge 선형회귀를 정말 잘 설명한 An Introduction to Statistical Learning 책이 있으니 한번 읽어 보시기를 추천 드립니다.

이제 베이지안 방법론을 이용하여 같은 결론을 어떻게 얻을 수 있을지 살펴 보도록 하겠습니다. 먼저 사후분포는 사전분포와 우도의 곱에 비례한다는 것을 기억하시기 바랍니다. 먼저 사전분포로 평균이 0이고 분산이 \(\tau^2\)인 정규분포로 가정합니다.

파란색이 우도, 초록색이 사전분포입니다. 이때 약간의 수식 변경을 통해

라고 표현할 수 있습니다. 이때 우리는 계수에 대한 최대값을 구하기로 했기 때문에 계수와 연관이 없는 항에 대해서는 제거할 수 있습니다.

또한 우도 대신 로그 우도 함수를 구해도 동일한 결과를 얻기 때문에

로 로그를 씌웁니다. 이것을 \(2\sigma^2\)로 곱하고 \(-1\)을 빼면

이 되고 \(−x\)을 극대화하는 것은 \(x\)를 최소화하는 것과 같기에 최종적으로

위와 같은 식을 얻을 수 있습니다. 이것은 바로 Ridge 선형회귀 모델과 동일하다는 것을 확인하실 수 있습니다. (\(\lambda\) 대신 \(\frac{\sigma^2}{\tau^2}\)) 이로써 저희는 Ridge 선형 회귀가 평균 0을 가진 가우시안 사전분포에 대해서 MAP 추정치를 구하는 것과 동일하다는 것을 알수 있었습니다. (이때 낮은 사전분포의 분산이 높은 \(\lambda\)값을 의미합니다.)

마치며

지금까지 frequentist와 bayesian 관점에서 선형 회귀 모델에 대해 알아 봤습니다. 마지막으로 제가 공부하면서 도움이 되었던 자료에 대해서 알려드리며 글을 마칩니다.

• An Introduction to Statistical Learning by James, Witten, Hastie and Tibshirani
• Gaussian Processes for Machine Learning by Rasmussen and Williams.
• Kevin Murphy’s Machine Learning - a Probabilistic Approach
• Cameron Davidson-Pilon’s Probabilistic Programming & Bayesian Methods for Hackers